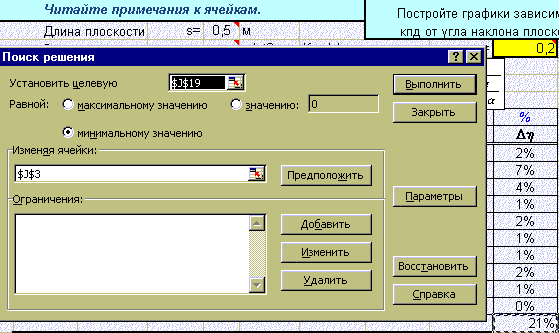
Использование опции "Поиск решения"
Итак, для нахождения
коэффициента трения надо добиться наилучшего совпадения графиков кпд,
полученных экспериментально и по теории (по формуле).
С математической точки зрения это означает, что надо минимизировать разность
кпд-практического и кпд-теоретического для каждого значения угла наклона
плоскости.
А точнее, надо минимизировать сумму этих разностей!
Таким образом, план таков:
1. Для каждого значения угла наклона ищем разность кпд-практического и
кпд-теоретического (можете называть это абсолютной ошибкой измерения);
2. Находим сумму полученных разностей;
3. Даем задание Excel'ю
подобрать такое значение коэффициента трения, чтобы эта сумма была наименьшей.
Приступаем.
1. В столбце J,
например, строим ряд значений разностей. Причем, обратите внимание на
то, что нам не важно то, в большую или меньшую сторону практическое значение
отличается от теоретического. Поэтому надо считать абсолютное значение
(модуль) разности:
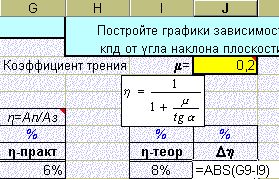
2. Ниже полученных данных записываем формулу их суммы:
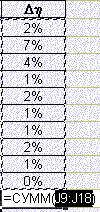
3. Выбираем в меню Сервис - Поиск решения.
В появившемся окне указываем, что в ячейке, содержащей сумму ошибок, надо
получить минимальное значение, подбирая коэффициент трения: